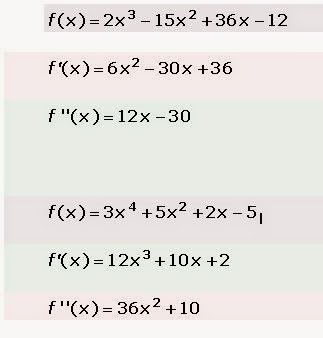Segunda Derivada
El Criterio o prueba de la segunda derivada es un teorema o
método del cálculo matemático en el que se utiliza la segunda derivada para
efectuar una prueba simple correspondiente a los máximos y mínimos relativos.
Al derivar la derivada de una función, derivada primera,
obtenemos una nueva función que se llama derivada segunda, f''(x).
Ejemplos:
- Diremos que una función es CÓNCAVA o presenta su concavidad hacia abajo cuando dados dos puntos cualesquiera el segmento que los une queda por debajo de la curva.
- Análogamente, diremos que es CONVEXA o presenta su concavidad hacia arriba si dados dos puntos de la curva el segmento que los une queda por encima de la curva.
- Los puntos en los que la curvatura pasa de cóncava a convexa o viceversa se llaman PUNTOS DE INFLEXIÓN.
Un punto de inflexión es un punto
donde los valores de x de una función continua pasa de un tipo de concavidad a
otra. La curva "atraviesa" la tangente. Matemáticamente la derivada
segunda de la función f en el punto de inflexión es cero, o no existe.
En el cálculo de varias variables
a estos puntos de inflexión se les conoce como puntos de ensilladura.
Máximos y Mínimos
Para esto debemos encontrar los puntos críticos los cuales se obtienen despejando "x" en la primera derivada.
Una vez obtenidos los puntos críticos, reemplazamos estos valores en la ecuación principal obteniendo as las coordenadas precisas de dichos puntos.
Aplicación en la Arquitectura.
Se las aplica cuando los
proyectos requieren de cálculos especiales que no se pueden obtener por
operaciones geométricas sencillas, al tener que calcular superficies
paraboloides o superficies orgánicas irregulares
Se necesita de las derivadas
para: máximos, mínimos, concavidad, convexidad, inflexiones de alguna figura
geométrica
Proyecto para el nuevo Museo de Arte Contemporáneo de Milán
Bibliografia: